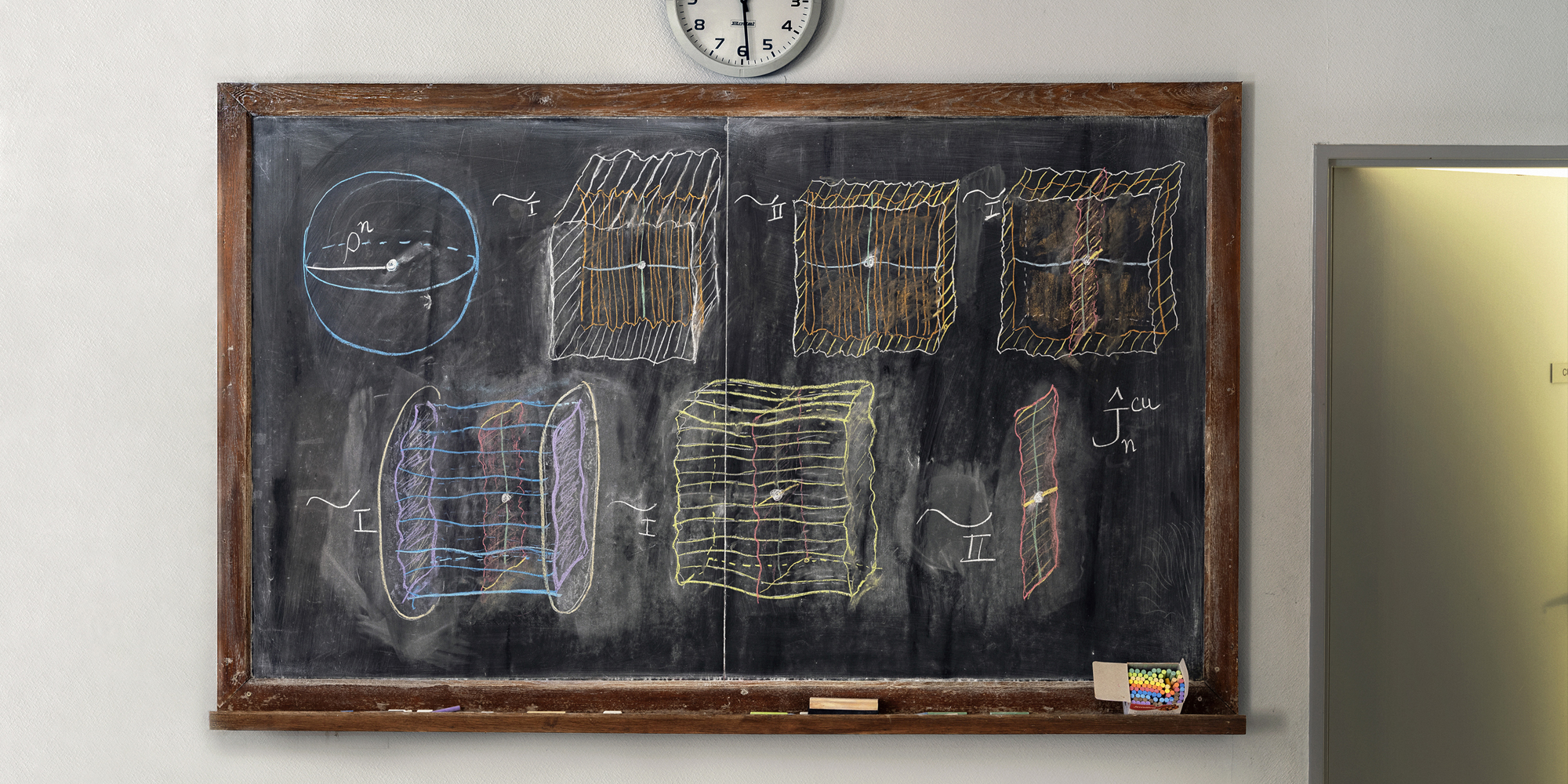
“On this blackboard is a central argument in a paper I wrote with Keith Burns (professor of mathematics, Northwestern University) about a mechanism for chaotic dynamics.”—Amie Wilkinson, Professor of Mathematics, University of Chicago (Photography by Jessica Wynne)
A photographer captures the beauty of mathematicians’ chalk experiments.
Artists have paintbrushes and canvas, carpenters have hammers and wood; for mathematicians, the tools of the trade have long been a blackboard and a slender cylinder of chalk (preferably Hagoromo, the cult-favorite Japanese brand celebrated in the profession for its durability and lack of dust).
“The boards are their homes, their labs, their private thinking spaces,” writes photographer Jessica Wynne in the introduction to Do Not Erase: Mathematicians and Their Chalkboards (Princeton University Press, 2021). The book features 110 images of chalk-based investigations by mathematicians around the world—several affiliated with UChicago, as shown in these pages —alongside their reflections on blackboards as a medium.
The project was sparked by married UChicago mathematicians Amie Wilkinson and Benson Farb, Wynne’s neighbors each summer on Cape Cod. One afternoon Wynne watched Farb at the dining room table jotting notes on paper (any port in a storm) and puzzling over symbols, drawings, and equations whose significance she couldn’t discern. Not understanding the notes made them feel more intriguing—like a glimpse into a secret world.
This memory returned to her as she reviewed a series of photos she’d taken in Jaipur, India, of lessons in Hindi inscribed on chalkboards at a local school. To her eyes the images had the same elegant, impenetrable quality as Farb’s calculations.
Wynne began writing to mathematicians at institutions near her New York City home, seeking permission to photograph their chalkboards. They could share new or completed projects; her only rule was no whiteboards or glass.
The mathematicians’ research itself remained mysterious to Wynne, but she came to see a connection between their work and hers. “They have a heightened aesthetic awareness, distinct styles and ways of using chalk, just like a visual artist,” she writes in Do Not Erase. “Some of the formulas are intensely chaotic, with explosive energy, while others feel neat, quiet, serene, and carefully considered.”
For all these individual differences, she was also struck by deep similarities as she took photos in the United States, Europe, and South America: math is the same everywhere, a common language pointing toward universal truth.
Do Not Erase attracted more participants than she expected, and Wynne found she rarely had to explain to her subjects why she was interested. “The mathematicians universally got it,” she says. “Their reaction was, basically, ‘Of course math is beautiful.’”
Amie Wilkinson
Professor of Mathematics, University of Chicago
“On this blackboard is a central argument in a paper I wrote with Keith Burns (professor of mathematics, Northwestern University) about a mechanism for chaotic dynamics. It depicts a sequence of shapes that, in a precise sense, are equivalent to each other, starting with a spherical ball and ending with something called a julienne, named for its resemblance to a thinly sliced vegetable. We are proud of this paper; as Keith likes to say, a good paper has one truly new idea, and this one has two.” (See photograph above.)
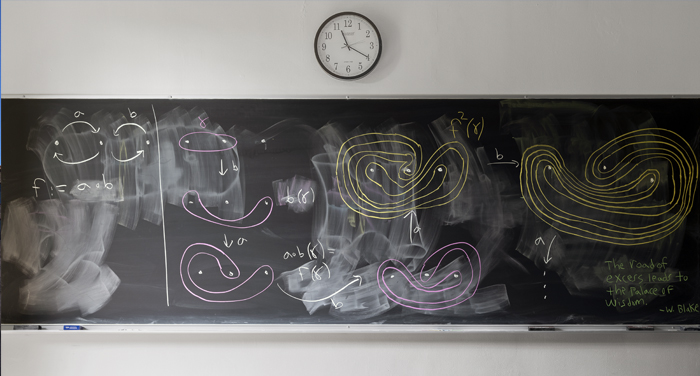
Benson Farb
Professor of Mathematics, University of Chicago
“The main tool that most of us use to communicate our ideas is the chalkboard. ... A computer doesn’t help much with 40,000 dimensions, but on a blackboard, I can work up a schematic of the situation, explaining it in real time to a student or collaborator. She can jump up and start writing on the board during my explanation, amending my computations, noting possible problems, unwrapping some equation into a flurry of computations of her own. Doing this dance at the blackboard with someone is an intense, frustrating, energizing, and sometimes moving experience.”
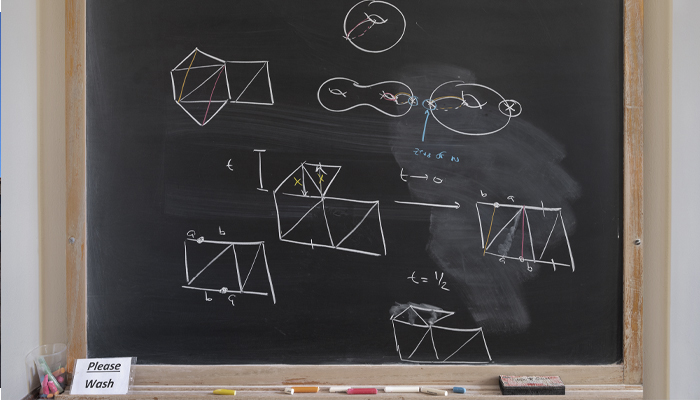
Paul Apisa, SM’14, PhD’18
Donald J. Lewis Research Assistant Professor, University of Michigan
“There are two axioms I would like to throw out that I imagine few people will object to: first, mathematics can be complicated; and second, humans think slowly—or, to make the second axiom less grandiose, I think slowly.
… A virtue of chalk, and talks that use it, is that it checks the Icarian desire of a speaker to communicate too much, heedless of the capacity of the listeners to comprehend. But perhaps the most important virtue of chalk is that it enables bad drawings. ... It forces you to draw cartoons that only capture the essential features of a complex system and forces you to think about exactly what those features are.”

Ana Balibanu, SM’13, PhD’17
Benjamin Peirce Fellow, Harvard University
“This chalkboard has a schematic outline of a project about a family of geometric objects called Hessenberg varieties. An individual Hessenberg variety can be very complicated—inscrutable, even. Instead, we have to consider all possible Hessenberg varieties together and understand the relationships between them. Their geometry then becomes clear through the way they interact. The diagrams on the board map out these interactions. ... The lists are speculations about which direction the results might take. (In hindsight, some of them are true and some of them are not.) The board is a snapshot of an exciting moment in the project—there are many uncertainties, but also many possibilities.”
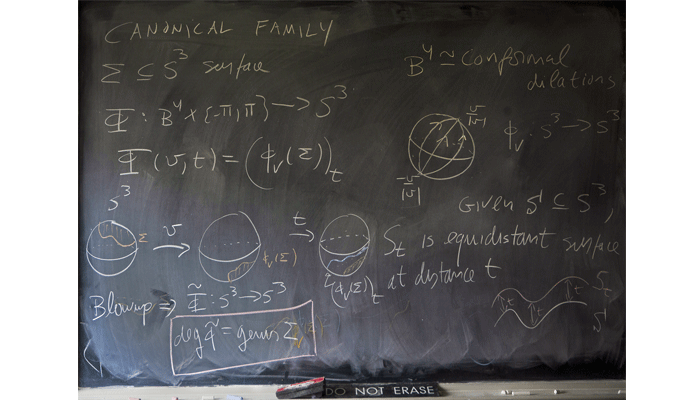
André Neves
Professor of Mathematics, University of Chicago
“The work on this blackboard was developed in part with my collaborator, Fernando Codá Marques, during a Thanksgiving dinner in Palo Alto in 2011. My wife and our soon-to-be three-year-old daughter and newborn son enjoyed the party while Fernando and I obsessed over the Willmore conjecture, a well-known problem that proposes what ought to be the ‘optimal’ shape among all doughnut-like shapes. Geometers love to think about these kinds of questions.”
Simion Filip, SM’12, PhD’16
Associate Professor of Mathematics, University of Chicago
“The blackboard is an active space, ready to change and willing to carry any thought. It doesn’t have the restricting linear quality of a written text, and it allows the user to organize the material according to its natural, spatial characteristics. Compared with writing on a page, the blackboard invites wider gestures and larger symbols. The broader physical space makes it psychologically satisfying to work on a blackboard.”

Clark Butler, SM’14, PhD’18
Veblen Research Instructor, Princeton University
“The blackboard depicted here was created during discussions with Jairo Bochi, a mathematician working at the Pontifical Catholic University of Chile. The left side hows some motivating discussion for the problem that we were considering. The right side is a collection of equations governing the phenomenon we were studying. The middle is a visualization we created that shows these equations in motion. We noted that it looks something like the pages of a book being flipped around its spine. … I think non-mathematicians would be surprised how concrete our thinking is, and how many analogies we draw to everyday objects and experiences.”
