
Barber’s work can be illustrated with these scans of a chicken wing. This image is the raw data collected by the CT sensors. (Image courtesy Taly Gilat-Schmidt)
A mixture of theory and practice helps statistician Rina Foygel Barber, SM’09, PhD’12, optimize her results.
For assistant professor Rina Foygel Barber, SM’09, PhD’12, statistics is “one of the fantastic places that you can get a real intersection between theory and application—not just in the same PhD program but in the same project.”
Take her research on image formation in computed tomography (CT) scans. In collaboration with Emil Sidky, SM’91, PhD’93, a research associate professor in radiology at UChicago, and Taly Gilat-Schmidt, a biomedical engineer at Marquette University, Barber used optimization theory to help develop the mirrored convex/concave (MOCCA) algorithm, which helps CT scanners make better, clearer three-dimensional CT images in less time.
A CT scan assembles a series of X-rays taken from different angles into one three-dimensional image, providing doctors with a more thorough picture of a patient than they’d see in a two-dimensional image. An algorithm controls the process of taking and assembling these images; the more efficient it is, the quicker the scanning process. A shorter CT scan not only saves time and money and reduces patients’ radiation exposure but also improves the scan itself—the longer patients have to lie still, the more likely they are to twitch or fidget, blurring the resulting image.
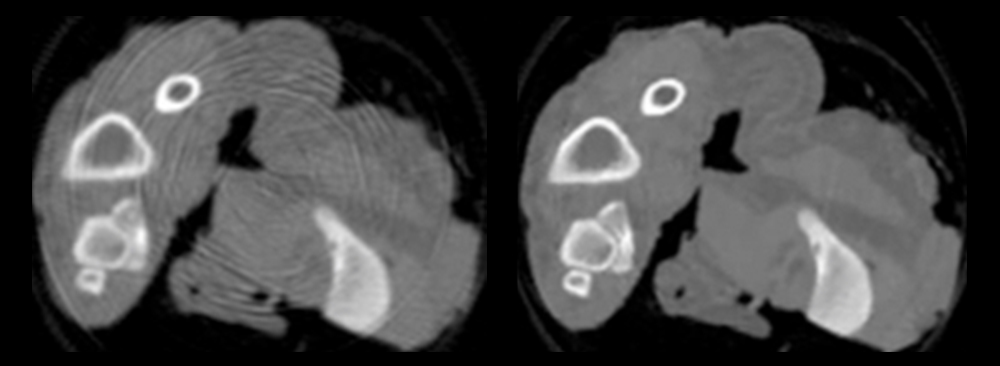
“We are working with real data and answering real questions,” says Barber, “but at the same time we’re learning about optimization theory and figuring things out that are much more general than just that specific problem.”
Optimization theory in statistics involves finding the equation that best answers the problem at hand. The trick is to avoid choosing a local optimum, which is the best option within a small neighborhood of possible solutions, instead of a global optimum, which is the best option period. Regarding convex and nonconvex (concave and linear) algorithms, convex means that an optimal solution is guaranteed to be the best global solution.
Because they avoid the trap of the local optimum, “almost all of the main theory and really beautiful theory” has been for convex optimizations, which Barber notes are also easier to work with. But CT scans and other medical imaging involve an element of randomness, as X-ray beams can behave unpredictably. This randomness, Barber and her team found, is better captured and accounted for with a nonconvex equation.
As they worked together on the MOCCA project, Sidky noted that unlike many theorists, who contribute one central idea to a collaboration and then leave the rest to the experimentalists, Barber “listens to all aspects of it: the experimental part of it and some of the issues I had for implementing on a large scale. She has ideas on all of those things.”
Barber attributes her involvement in the project—and to some extent, her career in statistics—to happenstance. After earning her undergraduate degree from Brown in 2005, she taught math at the Park School in Baltimore. Although she loved teaching, she says, “I just needed a bit more math in my life.” At the beginning of her second year in UChicago’s doctoral program in mathematics, she took a statistics course for fun and was hooked.
Her introduction to Sidky came in 2014, her first year on the faculty at UChicago. Some of Sidky’s students took Barber’s course on compressed sensing, another statistical area with medical imaging applications having to do with the minimum number of images required to produce, for example, a CT scan. Hearing about the course from his students, Sidky and other members of the radiology department met with Barber, and their work in CT image reconstruction quickly shifted from compressed sensing to nonconvex optimization.
Barber hopes that her work with Sidky and Gilat-Schmidt can not only find applications with other types of imaging but also “inspire completely different problems from the stat and math side.”
She is already making her mark in other subfields. In March she received the Institute of Mathematical Statistics Tweedie New Researcher Award for “groundbreaking contributions” in her work with her postdoctoral adviser, Stanford’s Emmanuel Candès, on what statisticians call a knockoff filter, which helps eliminate variables in a data set.
She also works on high-dimensional inference and estimation methods, which apply classical statistical techniques to data representing a much larger sample size than a traditional statistical sample.
Because high-dimensional statistics and large-scale optimization are relatively new subfields of statistics and thus, says Barber, “tend to skew younger,” she finds women to be well represented among her peers. At UChicago specifically, she notices strides in terms of gender diversity in math and science. “It’s been a great place to be from the start,” she says.
In fact, Barber’s graduate experience—along with the University’s collaborative research climate and proximity to her family—was a significant draw to come back as faculty.
