
(Image courtesy Charlie Smart and Wesley Pegden)
Associate professor Charles Smart summits the Abelian sandpile.
For a long time, scientists and mathematicians have tried to formulate theories that explain vastly different phenomena using a few simple rules. One such unifying theory is self-organized criticality, proposed to explain how complexity emerges, as in natural occurrences like forest fires, earthquakes, and species extinctions. Self-organization refers to how nonequilibrium systems naturally develop structures and patterns. Criticality references phase transitions and the border between stability and chaos.
The Abelian sandpile model, developed by statistical physicists in 1987, shows what happens when a pile of sand falls—a seemingly chaotic process that turns out to be quite orderly. Imagine grains of sand randomly dropped onto a square grid. When any square has at least four grains, the pile topples, sending one grain to each adjacent square and initiating a chain reaction of grains falling until each square has less than four.
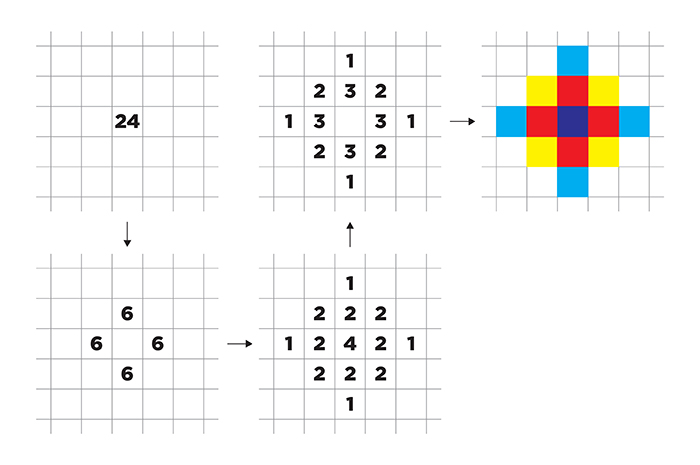
This stabilizing avalanche leads to complex fractal patterns that were long unexplained.

Over several years, UChicago associate professor Charles Smart, Lionel Levine (Cornell), and Wesley Pegden, AB’04 (Carnegie Mellon), combined their expertise in different mathematical fields to develop a precise explanation for the emergence of these patterns. They showed that no matter how many grains you start with, you end up with basically the same overall picture.
The mathematicians’ complete classification of the sandpile patterns appears in the May 2017 Annals of Mathematics. Their deeper understanding of how these models work could help predict and manage our seemingly—perhaps deceivingly—chaotic world.
